«
En
mathématiques,
on
ne
travaille
pas
sur
les
grandeurs
(c’est
l’objet
d’autres
disciplines,
comme
la
physique,
la
technologie,
les sciences de la vie et de la Terre ou la géographie et l’économie par exemple), mais avec les grandeurs ou à partir d’elles.
En mathématiques, on travaille dans le domaine des nombres
».
Programme de 3e. Place des grandeurs dans l’enseignement des mathématiques au collège.
On
a
déjà
vu
comment
construire
un
tableau
de
valeurs,
à
partir
d’une
situation
de
proportionnalité,
en
mettant
de côté les grandeurs et les unités.
La
tentation
est
forte
d’inverser
le
processus
pour
définir
directement
la
proportionnalité
à
partir
des
tableaux
en
écartant
définitivement
les
grandeurs
et
les
unités.
Il
n’y
a
alors
pas
d’autres
solutions
que
d’utiliser
les
valeurs
du
tableau
comme
dans
les
exemples
ci-contre
extraits
de
manuels de 5
ème
.
- Ce sont les lignes qui deviennent proportionnelles.
- Un seul coefficient apparaît.
- Le deuxième exemple montre que les propriétés de
proportionnalité ne sont valables que pour les cases qui
ont été vérifiées. On ne peut donc pas ajouter de
nouvelles colonnes sans une nouvelle vérification.
-
Plus
grave
d’un
point
de
vue
didactique,
les
deux
propriétés
de
base
de
la
proportionnalité,
la
bijection
et
la linéarité, sont occultées.
On ne peut pas établir la proportionnalité de deux grandeurs à partir d’un tableau.


E
n
fait,
en
regardant
les
exercices
corrigés
de
ces
manuels,
on
s’aperçoit
que
l’on
ne
demande
jamais
aux
élèves
de démontrer que deux grandeurs sont proportionnelles, il suffit qu’ils l’affirment … ou pas.
Non ? Pourtant de nombreux manuels osent le grand saut.
Des grandeurs proportionnelles aux tableaux
Les tableaux
Des tableaux aux grandeurs proportionnelles
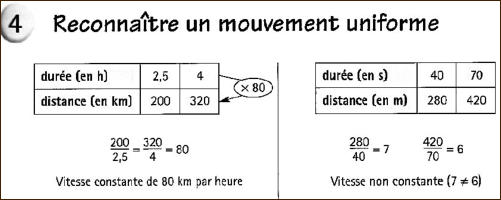
La
durée
et
la
distance
étant
des
grandeurs
continues,
elles
admettent
une
infinité
de
valeurs.
Conclure
à
une
vitesse
constante
à partir de deux valeurs est une erreur
très grave
en mathématique.
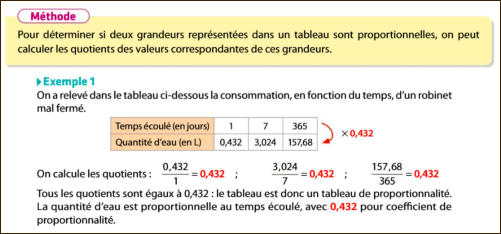
Passons
sur
ces
mathématiciens
qui
laissent
couler
un
robinet
mal
fermé
pendant
1
an,
passons
aussi
sur
la
méthode
de
mesure
et
l’étrange
précision
des
résultats,
car
même
si
ce
tableau
est
un
tableau
de
proportionnalité,
on
ne
peut
pas
conclure
que
les
grandeurs sont proportionnelles.
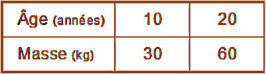
A
partir
de
ce
tableau,
allez
vous
conclure
que
la
masse
de
cette
personne
est proportionnelle à son âge et qu’elle pèsera donc 180 kg à 60 ans ?

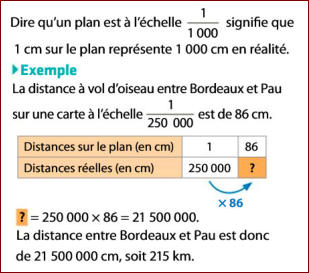




Les situations rencontrées sont des grands classiques qui donnent lieu à une étude spécifique :
les prix à l’unité, les pourcentages, les échelles, les vitesses.
Pour
chacune
d’elle,
l’élève
doit
connaître
des
procédures
qui
donnent
la
solution
et
servent
en
même temps de justification. La référence à la proportionnalité n’est même pas nécessaire.
On
retrouvera
la
même
chose
en
géométrie
où
la
proportionnalité
est
cachée
derrière
des
formules,
sans oublier le cas très particulier du théorème de Thales.