
Les fractions offrent d’autres méthodes de calcul qui s’appuient sur le partage en 100 parties égales.
On peut par exemple, commencer à calculer la valeur de 1 % du capital.
Une quantité fixe est partagée en plusieurs parties distinctes.
On construit par proportionnalité, une nouvelle répartition
pour un total égal à 100 unités.
Les fractions sont ainsi conservées :

Aujourd’hui,
où
les
pourcentages
constituent
l’essentiel
de
notre
information
chiffrée
dans
les
médias,
leur
enseignement est devenu un enjeu citoyen.


Les
problèmes
dits
de
«
pourcentages
»,
ne
se
caractérisent
pas
par
le
signe
%
qui
peut,
à
volonté,
être
remplacé
par
un
décimal
ou
une
fraction,
mais
par
des
situations de proportionnalité particulières.

Les proportions

Dans
cette
situation,
deux
grandeurs
proportionnelles
homogènes,
exprimées
dans
la
même
unité,
sont
reliées
par
un
coefficient
fixe.
Toutes
les
méthodes
de
recherche
de
quatrième
proportionnelle
peuvent
être
utilisées.
Par exemple
:
Il y a trois situations couramment utilisées pour introduire les pourcentages : les proportions, les fractions et les quantités.
Quel intérêt va vous rapporter au bout d’un an, un capital de 240 € placé au taux annuel de 5 % ?
Exemple
:
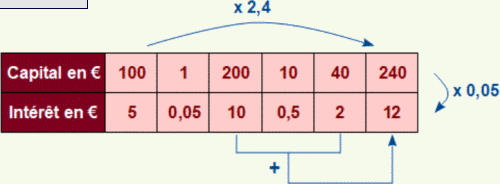
100 € rapportent 5 €
200 € rapportent 10 €
10 € rapportent 0,50 €
40 € rapportent 2 €
200 € + 40 € rapportent 10 € + 2 €
240 €
:
100 € = 2,4
5 € x 2,4 = 12 €
240 € x 0,05 = 12 €
Les formules du type :
Intérêt
annuel
=
Capital
x
Taux
sont
un
objectif
important
à
atteindre
et
doivent
donc
être
présentées
assez
tôt,
mais
elles
demandent
une
certaine
familiarité
avec
la
multiplication
et
la
division
par
un
décimal,
qui
ne
sont
pas
abordées avant la 6
ème
.
De
plus,
il
n’existe
pas
de
noms
génériques
comme
pour
les
vitesses
(
Distance
=
Vitesse
x
Temps
)
et
chaque
situation
a
son
vocabulaire propre (
Prix TTC = Prix HT x Taux
) suivant les grandeurs en jeu et les appellations données aux proportions :
pourcentage, proportion, fraction, quotient, taux, coefficient, fréquence, pente, …
Exemple
:
Calcul mental
Un calcul mental direct, sans passer par les tableaux, est une faculté essentielle
pour estimer un pourcentage ou contrôler les résultats d’une calculatrice.
On peut utiliser un calcul de fraction en prenant 10 % comme pivot.


240 €
:
100 = 2,40 €
2,40 € x 5 = 12 €

Dans
cette
situation,
on
retrouve
un
tableau
de
proportionnalité
mais ici c’est le capital qui reste fixe et c’est le taux qui varie.
Les quantités
10 % de 240 € = 240 € : 10 = 24 €
5 % de 240 € = 24 € : 2 = 12 €
30 % de 240 € = 24 € x 3 = 72 €
35 % de 240 € = 72 € + 12 € = 84 €




En
plaçant
un
capital
de
240
€
au
taux
de
5
%,
quel
sera
le
montant
de l’intérêt au bout d’un an ?
A
quel
taux
faut-il
placer
un
capital
de
240
€
pour
obtenir
un
intérêt
de
12 € au bout d’un an ?
Quel
capital
faut-il
placer
au
taux
de
5
%
pour
obtenir
un
intérêt
de
12 € au bout d’un an ?
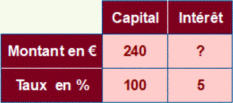
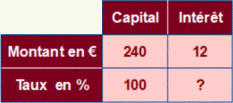
Ces tableaux de proportionnalité ont l’avantage de mettre en évidence les grandeurs en jeu et la structure du problème.
Suivant la valeur manquante, on distingue trois types de problèmes.


Ce
sont
peut-être
ces
difficultés
qui
amènent
les
manuels
de
collège
à
réduire
au
maximum
le
cours
sur
les
pourcentages
et
il
n’en
reste
pas
grand
chose.
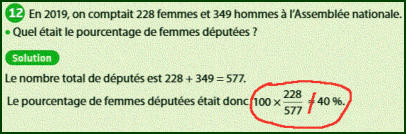
L’exemple ci-contre représente tout ce qu’on y trouve.
On n’y présente que des procédures sans indiquer à quoi elles s’appliquent.
Quelles sont les grandeurs en jeu et quel est le nombre à multiplier ?
On
y
parle
bien
de
proportionnalité
mais
dans
les
exemples
fournis,
il
n’y
a
pas
de
grandeurs
proportionnelles.
Certes
cela
marche
bien
quand
il
n’y
a
que
deux
nombres dans le texte du problème mais est-ce seulement cela l’objectif ?
La
deuxième
définition
assimile
un
pourcentage
à
une
proportion
écrite
sous
forme d’une écriture fractionnaire de dénominateur 100
.
Mais qu’est-ce qu’une proportion?
Vous pouvez chercher dans tous les manuels, on n’y trouve aucune définition.
L’exemple montre que pour l’auteur c’est une fraction.
Toute cette phraséologie revient donc à dire : un pourcentage est une fraction.
L’expression un taux de t % peut être source de confusion
car le taux n’est pas t mais t %
Certains auteurs se prennent même les pieds dans le tapis :

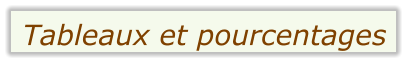
Quel est le pourcentage des élèves externes de 3
ème
?

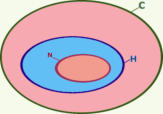
Cette représentation offre l’avantage de relier clairement les trois pourcentages de chaque catégorie.
Les tableaux croisés additifs
tableaux de pourcentages
Un calcul de pourcentage ne se résume pas à choisir et appliquer la bonne opération,
le choix des nombres est au moins aussi important mais pas toujours très simple.
Il s’agit là d’une question pour le moins ambiguë
qui recouvre trois réponses possibles :
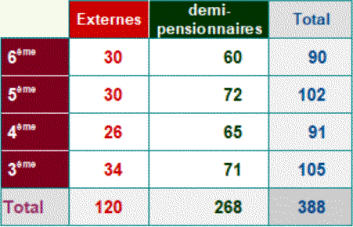

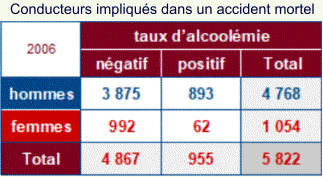

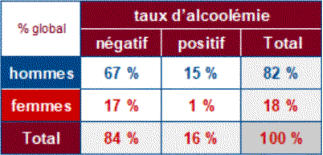

On peut regrouper tous les pourcentages dans trois tableaux distincts.
Dans chacun d’eux les pourcentages s’ajoutent pour obtenir les 100 % du total utilisé.
Pour chaque tableau, imaginez la phrase commencée et cliquez dessus pour voir une solution.
manuel de 5
ème
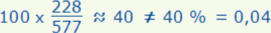

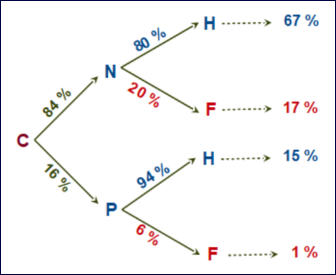
Les arbres
Lecture
: 84 % des conducteurs impliqués dans un accident mortel ont un taux d’alcoolémie négatif.
80 % d’entre eux sont des hommes soit 67 % des conducteurs impliqués dans un accident mortel.
C’est une propriété des inclusions successives.
84 % x 80 % = 67,2 %
et ce n’est pas là un hasard, comme le montre le calcul exact avec les fractions :
ou même de façon plus formelle :

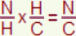
67 % + 15 % = 82 %
81 % + 19 % = 100 %
80 % + 94 % n’a pas de sens
car les pourcentages ne portent
pas sur le même total.
Aux dernières élections à Clochemerle les résultats ont été les suivants :
Le taux de participation est de 70 %. 20 % ont voté blanc ou nul. La liste A a obtenu 55 % des suffrages exprimés.
Quelle est la proportion des électeurs qui ont voté pour la liste A ?
Application
Il
en
découle
une
multitude
de
procédures
de
calcul,
ce
qui
n’est pas toujours un avantage ( voir
4ème proportionnelle
).
Construire
un
tableau
et
traîner
le
nombre
100
dans
les
calculs
devient très lourd pour la suite.
Un soir de dépouillement électoral,
je vois mon voisin qui tape plusieurs opérations sur sa
calculatrice pour obtenir un pourcentage.
Il m’explique : « je divise le total par le nombre de voix
puis je divise 100 par le résultat.»
Je lui fait remarquer qu’il y a plus simple.
«On me l’a déjà dit, mais ça je suis sûr que ça marche !»
Les fractions











