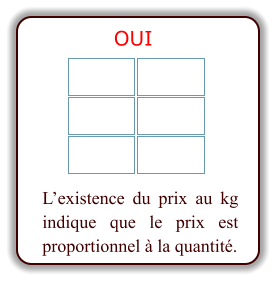
la multiplication par un décimal

volume
hauteur
60 L
45 cm
50 L
?

Les fonctions linéaires ( 2 réponses)
Ce problème a été proposé à des professeurs de mathématiques en dernière année de formation.
Il leur était demandé de décrire leurs procédures personnelles
sans considération pédagogique
.
Un aquarium en forme de parallélépipède rectangle de 45 cm de haut a un volume de 60 litres.
Quelle sera la hauteur d'eau si on n'y verse que 50 litres ?
1°) Reconnaître
2°) Calculer
3°) Enseigner
Si
une
voiture
parcourt
100
km,
en
1
h
35
min,
quelle
distance
parcourra-t-elle en 2 h ?
J'ai payé 2,54 € un morceau
de fromage de 147 g.
Quel est le prix au kilo ?
Le
médecin
prescrit
80
ml
de
Mannitol
à
passer
en
20
minutes
à
l’aide
d’un
perfuseur
de
préci
-
sion
(1
ml
=
60
gouttes).
À
quel
débit
[gouttes/min]
l’infirmier
doit-il régler la perfusion ?
Saurez-vous dire si ces problèmes relèvent de la recherche d’une 4
ème
proportionnelle ?
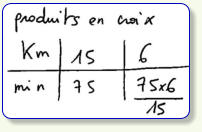
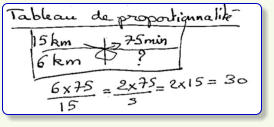
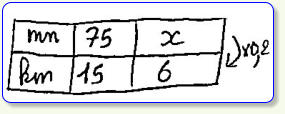
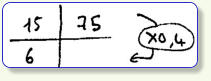
Un coureur à pieds a couru à la même vitesse
pendant 75 min. Il a parcouru 15 km.
Combien de temps a-t-il mis pour parcourir 6 km ?
Si
vous
pouvez
acheter
12
paquets
de
gâteaux
à
9
€
le
paquet,
combien
pouvez-vous
acheter de paquets à 3 € ?










Les grandeurs quotients ( 26 réponses)
La linéarité ( 22 réponses)
Les coefficients de proportionnalité ( 23 réponses)
Les passages par l’unité ( 27 réponses)
Le produit en croix ( 43 réponses)

Le certificat d’études
Xavier DARCOS ministre de
l’Education Nationale
La règle trois
On
observe
une
multitude
de
procédures
que
l’on
peut
classer
en
six
grandes
catégories
auxquelles
il
faut
rajouter une grande variété dans le traitement des grandeurs et des unités.
Cette
grande
diversité
peut
être
un
avantage
pour
ceux
qui
la
maîtrisent,
mais
c’est
surtout
une
source
de
grandes difficultés dans l’enseignement :
Pour l’enseignant, comment corriger un tel exercice ?
Quelle procédure privilégier quand le programme demande de s’appuyer sur les procédures des élèves ?
Pour les parents qui veulent expliquer la procédure qu’ils maîtrisent et qui n’est plus celle qui est
utilisée en classe car les programmes évoluent constamment.
Pour les élèves qui doivent s’adapter tous les ans au changement de professeur et de méthode.
Ce peut être un enrichissement pour certains mais c’est un blocage pour beaucoup.
( Cliquez sur les images pour obtenir la réponse )
Cette
procédure
(
à
ne
pas
confondre
avec
la
règle
de
trois
)
qui
s'appuie
sur
des
propriétés
algébriques,
n'a
aucune
signification
en
termes
de
grandeurs
(
6
km
x
75
min
ne
correspond
à
rien).
Elle
est
perçue
par
les
élèves
comme
un
"truc" qui leur donne le résultat recherché mais sans qu'ils sachent pourquoi.
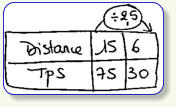
Il est à noter que personne n’a calculé la distance parcourue en 1 min.
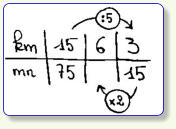
15 km x 5 = 75 km

Ingrédients : On sait que l'on a deux grandeurs proportionnelles.
On en connaît deux valeurs correspondantes.
On veut calculer la valeur correspondante à la troisième valeur connue .
La
recherche
d'une
4
ème
proportionnelle
occupe
une
place
particulière
dans
l'apprentissage
de
la
proportionnalité
car elle est considérée comme le problème le plus simple. En fait, elle en contient déjà toutes les difficultés.
BILAN
En général, les unités ne sont inscrites qu’au résultat.
Les
problèmes
de
recherche
de
quatrième
proportionnelle
peuvent
être
abordés
très
tôt
en
choisissant
des
nombres
adaptés
au
niveau
des
élèves.
On
peut
obtenir
la
solution
en
passant
par
l’unité,
sans
aucune
référence
explicite à la proportionnalité.

masse
prix
1 kg
4 €
?
28 €


masse
prix
4 kg
24 €
1 kg
?


masse
prix
1 kg
4 €
3 kg
?

Les situations de proportionnalité sont employées très tôt dans l’enseignement, elles apparaissent avec la multiplication.
En effet, si une des valeurs connues est égale à 1, on retrouve les trois problèmes de base du bloc multiplicatif.


Quel est le prix de 4 kg
de pommes à 2,40 € le kg ?
Quel est le prix de 2,4 kg
d’oranges à 4 € le kg ?
Pour le premier problème, il s’agit de multiplier par 4 :
4
x
2,40 € = 2,40 € + 2,40 € + 2,40 € + 2,40 € = 9,60 €.
La multiplication par un entier est une addition répétée.
Pour le second, la multiplication par 4 ne donne pas la solution.
4
x
2,4 kg = 2,4 kg + 2,4 kg + 2,4 kg + 2,4 kg = 9,6 kg
On ne peut pas trouver des euros en ajoutant des kg.
Il faut donc donner du sens à 2,4
x
4 €.
Nous avons déjà vu que, si pour ces deux problèmes le calcul est identique ( 4 x 2,4 ), ils ne sont pas de même nature.
La
difficulté
de
ces
problèmes
est
très
dépendante
des
nombres
utilisés.
Les
nombres
décimaux
par
exemple,
sont
un
obstacle
insurmontable
pour
beaucoup
à
l’école
primaire,
comme
le
montre
ces
tests
effectués
en
début
de
collège.
La
multiplication
et
la
division
par
un
décimal,
puis
la
multiplication
des
fractions
pourtant
nécessaires à une présentation globale de la proportionnalité ne sont abordées respectivement qu’en 6
ème
et 5
ème
.
Il n’est donc pas possible d’aborder une théorie de la proportionnalité avant le niveau 5
ème
.



La proportionnalité permet une première méthode de calcul par linéarité en décomposant les quantités.

Par exemple pour 2,358 kg
2 x 7 € + 3 x 0,70 € + 5 x 0,07 € + 8 x 0,007 €
ou
2 358 x 0,007 €
en passant par 1 g
Après cette première phase, on peut introduire l’idée de multiplication et ses règles de calcul classiques
en s’appuyant sur l’égalité numérique 2 358 x 0,007 = 2,358 x 7
On peut alors parler de multiplication entre les grandeurs : prix = quantité x prix à l’unité
Ces exercices utilisant des factures renforcent cette structure
en insistant sur l’identification des grandeurs.
( l’utilisation d’une calculatrice permet de se dégager de l’influence des nombres )
Interrogation écrite
Gilbert Lafaille