Pour commencer un petit exercice d’échauffement avec un grand classique de la proportionnalité.

Quelle est l’échelle de cette carte de 40 cm sur 30 cm ? Rappel : l’équateur mesure 40 000 km.

Réponse Cette carte est obtenue par une projection de Mercator. Comme toutes les cartes terrestres, elle est déformée, car il est impossible de mettre une sphère à plat sans déformation. Le calcul d’une échelle n’a donc pas de sens car 1 cm sur la carte ne représente pas toujours la même longueur sur la Terre.

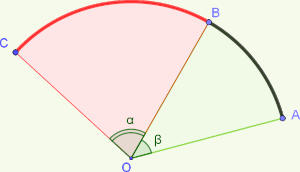
Les cordes et les arcs dans un cercle de centre O La première condition est respectée : si les angles au centre sont égaux, les cordes et les arcs interceptés sont égaux.

En conclusion La proportionnalité est une propriété intrinsèque aux grandeurs, nul besoin de mesures, de calculs, de tableaux ou de coefficients pour la démontrer.

- LE MOUVEMENT UNIFORME Deux distances égales sont parcourues en des temps égaux et réciproquement. Un intérêt essentiel de cette relation entre deux grandeurs proportionnelles est qu'elle permet de nous dispenser de raisonner sur les objets pour se placer directement dans le cadre des grandeurs. En effet, inutile d'identifier la portion du trajet qui mesure par exemple 12 km, puisque le temps de parcours est le même pour tous les tronçons de 12 km. - LES RECETTES DE CUISINE Elles sont données en général pour 4 personnes. Si ce n'est pas le cas, on calcule les nouvelles quantités en considérant que les quantités sont proportionnelles au nombre de convives, ce qui revient à dire que tous les convives ont le même appétit. Quand il y en a pour quatre, il n'y en a pas pour cinq. - LES MÉLANGES Si la soupe a été bien remuée, une cuillerée suffit pour savoir si la soupe est trop salée, elles contiennent toute la même quantité de sel. C’est ce qu’on appelle un échantillon représentatif. - LES PARTAGES ÉQUITABLES L'équité pourra être que chacun reçoive la même somme, mais aussi que chacun reçoive selon son travail ( à travail égal, salaire égal ) ou selon le capital investi. La proportionnalité devient alors la règle de calcul et justifie trop souvent le choix effectué … c’est mathématique ! On voit sur ces exemples que la proportionnalité est souvent synonyme d'équité, de régularité, d'homogénéité, d'équivalence ...

L’exemple précédent indique tous les ingrédients nécessaires pour avoir une situation de proportionnalité : Le cadre : - Un ensemble ‘‘ d’objets ’’ : l’ensemble de tous les chemins à vol d’oiseau sur Terre. - 2 grandeurs additives : la longueur réelle de ces chemins et leur longueur sur la carte. Les deux relations : la bijection entre les deux ensembles de grandeurs. la linéarité, c’est à dire la compatibilité entre les additions.

Il manque ici, la deuxième propriété nécessaire pour une situation de proportionnalité. Les temps de séchage ne s’ajoutent pas, les quatre chemises sécheront ensemble en deux heures.

En résumé Deux grandeurs m (masse) et p (prix) sont proportionnelles si et seulement si : Traduction Bijection : m 1 = m 2 est équivalent à p(m 1 ) = p(m 2 ) deux masses égales ont le même prix Linéarité: p(m 1 + m 2 ) = p(m 1 ) + p(m 2 ) le prix d’une somme est la somme des prix On peut montrer que la deuxième condition est équivalente à une forme multiplicative plus efficace dans les calculs : Linéarité : k étant un nombre p(k x m) = k x p(m) si on multiplie une grandeur par un nombre, l’autre est multipliée par le même nombre

AC < AB + BC La deuxième condition n’est pas respectée. La longueur de la corde n’est donc pas proportionnelle à l’angle au centre. Son calcul, plus complexe, est à l’origine de la trigonométrie.

La deuxième condition est respectée. La longueur de l’arc est donc proportionnelle à l’angle au centre. On peut la calculer facilement à partir du périmètre du cercle.

Exemple :