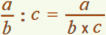Nous
avons
vu
que
les
fractions-partages
permettent,
dans
des
cas
simples,
d’aborder
des
règles
de
calcul
propres
aux
quotients
mais
si
on
continue
dans
cette
voie,
les
énoncés
proposés
deviennent
rapidement
artificiels
et
frisent
souvent le ridicule.

Pour
les
Grecs,
les
nombres
commensurables
étaient les seuls qu'on pouvait atteindre.
Il
est
clair
que
c'est
une
survivance
de
ces
idées
périmées
qui
nous
fait
tant
tenir
aux
nombres
commensurables,
nous
nous
cramponnons
à
eux
comme
aux
seuls
vestiges
d'un
enseignement
disparu.
Ne
faudrait-il
pas
mieux
reconnaître
qu'il
n'y
aurait
aucun
scandale
à
supprimer
le
chapitre
sur
les
fractions,
car
on
sera
bien,
je
pense,
d'accord
avec
moi
pour
déclarer
que
marier
des
22
èmes
et
des
37
èmes
est
un
martyre
que
nous
infligeons
aux
gosses
de
douze
ans
par
pur
sadisme,
sans
aucune
raison
d'utilité
comme
circonstance
atténuante.

Une
fraction
est
un
quotient
.
C’est
ce
point
de
vue
qui
doit
transparaître
au
travers
des
problèmes
de
divisions, de grandeurs quotients, de proportions, dans l’organisation des calculs et le calcul mental.
L’Arithmétique est le chapitre consacré à la recherche des diviseurs communs.
Après 30 ans d’absence, il est réapparu en 5éme en 2016.
Les simplifications sont une occasion de faire le lien avec la division au cours d’activités de calcul mental.
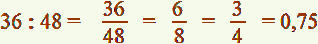

Pierre, Paul et Jacques doivent se partager équitablement 2 baguettes pour leur pique-nique.
Comment peuvent-ils effectuer ce partage ?
Solution : ils partagent chaque baguette en trois parts égales et chacun en prend deux.
2 : 3 =
Les divisions
Les simplifications
La proportionnalité
Un marchand achète 45 douzaines d’œufs pour 99 €. Il les revend 3 € la douzaine.
Quel est son bénéfice sur chaque douzaine ?
Indiquez la réponse sans effectuer les calculs.

Demander
les
solutions
en
écriture
algébrique
met
en
évidence
des
équivalences
entre
les
calculs
et permet de choisir le plus simple ou d’éviter les valeurs approchées.
L’écriture algébrique
Calculez 36 : 48 puis vérifiez à la calculatrice.

solutions :
ou
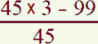
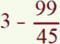


Un coureur à pieds a couru à la même vitesse
pendant 75 min. Il a parcouru 15 km.
Combien de temps a-t-il mis pour parcourir 6 km ?
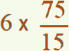
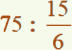
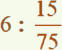
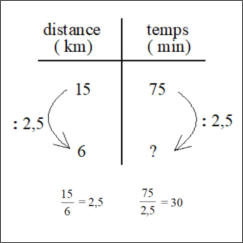

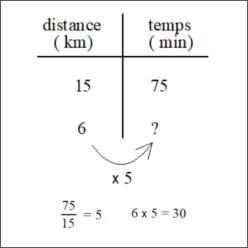
Parmi les nombreuses solutions, en voici trois possibles.
Les opérateurs multiplicatifs
=
=

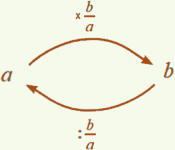
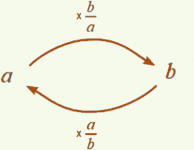
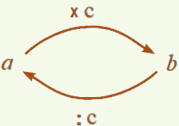
a : b : c = a : ( b x c )
L’exemple de la proportionnalité montre l’intérêt des opérateurs pour une visualisation dynamique des calculs.
On trouve le même bénéfice à les utiliser pour illustrer les propriétés des divisions comme inverse des multiplications.
Ces propriétés ne dépendent pas des nombres utilisés.
On peut les représente par des lettres, chaque lettre pouvant être remplacée par un nombre réel ( sauf peut-être le zéro.)
Définition
b : c = a
est équivalent à
a x c = b
ce qui peut être représenté par
et traduit par
La division est l’opération inverse de la multiplication
Écriture fractionnaire
Par convention d’écriture on a
c = b : a =
et donc
a x = b
et inversement
b x = a
Diviser par un nombre c’est multiplier par son inverse
Divisions successives
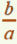
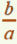
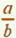
or d’après la définition