Accueil

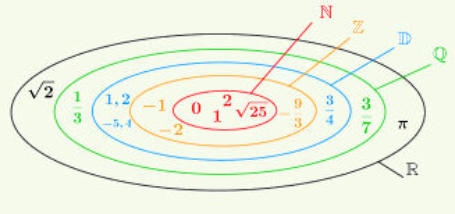
ℕ L’ensemble des nombres entiers C’est le socle sur lequel on construit tous les autres nombres. ℤ L’ensemble des nombres relatifs Le double de ℕ qui rend possible toutes les soustractions. ⅅ L’ensemble des nombres décimaux Ils s’écrivent avec un nombre fini de chiffres, ce qui permet de les utiliser en pratique pour mesurer les grandeurs et effectuer les calculs numériques. Ils sont souvent mal considérés car on les associe à l’idée de valeurs approchées. ℚ L’ensemble des nombres rationnels ( On les appelle aussi fractions ) Ils rendent possible les divisions de nombres entiers. ℝ L’ensemble des nombres réels Il existe une infinité de nombres comme √2 ou ℼ par exemple, qui ne sont pas des fractions. Ces nouveaux nombres acceptent une écriture décimale illimitée dont on ne peut connaître au mieux, que les premiers chiffres. On les appelle les nombres irrationnels. Si on les regroupe avec les nombres rationnels, on obtient l’ensemble des nombres réels.

Les priorités opératoires

Tous ces ensembles de nombres sont emboîtés comme des poupées russes. ℕ ⸦ ℤ ⸦ ⅅ ⸦ ℚ ⸦ ℝ

Quel est le plus grand nombre plus petit que 1 ?

N.B. : Les ensembles de nombres ne sont pas au programme du collège.

réponse

La solution d’un problème, s’obtient en général à l’aide de plusieurs opérations. Il existe plusieurs façons de les écrire.

Le compte est bon

Exemple

une écriture à étages telle que peut représenter 2 calculs différents.

Des ambiguïtés :

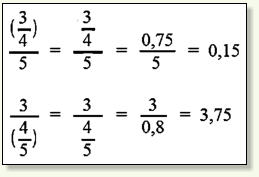
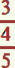
Comme le montre cet exemple, on peut lever l’ambiguïté en rétablissant des parenthèses ou en différenciant les barres de fractions par leur largeur et leur position.

Certains estiment ces méthodes peu fiables avec des élèves, ils préfèrent n’utiliser qu’une barre de fraction et un autre signe de division.

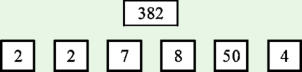
Il existe 4 façons différentes de noter les divisions : 2:3 2/3 2÷3 Avec l’écriture fractionnaire, on profite d’une dimension supplémentaire qui offre une vue d’ensemble plus claire de la structure du calcul. exemple : Malheureusement, elle n’est pas disponible sur les machines. On doit y rentrer les calculs sur une seule ligne comme par exemple sur le tableur OpenOffice L’oubli des parenthèses est une cause fréquente d’erreur.

l’histoire des notations

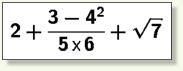
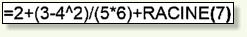
Le cas des divisions

8 x 50 = 400 2 + 7 = 9 9 x 2 = 18 400 - 18 = 382

( 8 x 50 ) - [ ( 2 + 7 ) x 2 ]

LES Priorités opératoires 1) Les opérations entre parenthèses. 2) Les puissances. 3) Les multiplications et divisions dans l’ordre d’écriture. 4) Les additions et soustractions dans l’ordre d’écriture.

8 x 50 - ( 2 + 7 ) x 2

le calcul détaillé

l’écriture en ligne

l’écriture algébrique

Avec l’écriture en ligne, le calcul ne peut pas se faire de gauche à droite, on indique l’ordre des opérations par des parenthèses. L’écriture algébrique rend l’écriture plus lisible en évitant l’accumulation de parenthèses. Elle utilise des règles de priorité adoptées par la communauté mathématique et implantées dans la plupart des calculatrices.

Les calculs approchés

Les valeurs approchées En mathématiques, du primaire au lycée, les problèmes proposés se situent dans un monde virtuel où toutes les mesures sont exactes. Aucune place pour l’incertitude. Et pourtant ! Les difficultés commencent avec le calcul des divisions qui ‘‘ne tombent pas juste ’’ et débouchent le plus souvent sur un développement décimal illimité. Viendront ensuite les nombres irrationnels, avec les racines carrées ou la trigonométrie. = 0,428571… π ≈ 3,14159… = 1,732050… cos 30° = 0,866025… ( Les trois points indiquent que tous les chiffres sont exacts. ) En pratique on utilise des arrondis car la calculatrice fournit souvent trop de chiffres pour la précision demandée. ≈ 0,43 π ≈ 3,1416 ≈ 1,732 cos 30° ≈ 0,866 En dehors de toute autre information, on suppose qu’un arrondi est une valeur approchée au plus proche. a ≈ 2,23 signifie donc 2,225 ≤ a < 2,235

Les calculs approchés

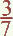
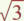
S i tous les calculs finis, exacts, les seuls qu'admettaient les Anciens, ont conservé toute leur importance mathématique, s'ils doivent être connus et étudiés par les mathématiciens actuels, leur importance pratique a considérablement diminué, et est parfois disparue totalement. Partout ces calculs, dits exacts, ont été détrônés par les calculs approchés et souvent les calculs exacts ne sont considérés que parce qu'ils conduisent au mode le plus simple de calcul approché. Henri Lebesgue (1875-1941)

Les calculs exacts

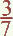
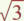
Exemple : a ≈ 2,23 b ≈ 2,64 2,23 x 2,64 = 5,8872 Quel crédit peut-on accorder à 5,8872 ? 2,225 x 2,635 ≤ a x b < 2,235 x 2,645 soit 5,862875 ≤ a x b < 5,911575 en arrondissant a x b ≈ 5,9

Dans cet exemple, le résultat comporte cinq chiffres mais il n’y en a que deux qui sont significatifs , les autres n’apportent aucune information, ils donnent même l’illusion d’une précision inexistante.

Les calculs à partir de valeurs approchées sont très incertains.

Un calcul exact est un calcul qui n’utilise aucune valeur approchée. Il est souvent possible d’y arriver en changeant l’ordre de calcul grâce à des propriétés des opérations indépendantes des nombres utilisés , autrement dit, valables pour tous les nombres réels. Ces propriétés, utilisées très tôt pour les calculs élémentaires et le calcul mental, deviendront incontournables pour le calcul littéral. En voici quelques exemples :

ce qui peut se décliner par : Pour multiplier un quotient par un nombre, on multiplie le numérateur par ce nombre. ou inversement Pour diviser un produit par un nombre, on divise un seul des deux facteurs par ce nombre.

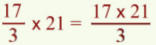
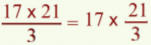
les racines carrées

les quotients

On peut inverser l’ordre entre multiplication et racine carrée.

les calculs avec π

Certaines calculatrices de collège possèdent un module calcul formel capable d’effectuer des calculs exacts avec les fractions, les racines carrées ou π dans des cas simples.

- On peut inverser l’ordre entre les multiplications et les divisions. (17 : 3 ) x 21 = (17 x 21) : 3

= 17 x 7 = 119

Pour beaucoup d’élèves, un nombre c’est ce qui s’affiche sur la calculatrice. Pourtant l’ensemble de tous les nombres que l’on peut y afficher ne représente même pas une goutte d’eau dans l’immensité infinie des nombres réels .

Les calculatrices numériques

Elles utilisent des nombres de plus de dix chiffres pour gagner en précision, mais aussi précises soient-elles, il ne s’agit que de calcul approché. Cependant, elles parviennent souvent à afficher la réponse exacte grâce à leurs chiffres en réserve.

Dans cet exemple, la calculatrice n’affiche pas tous les chiffres, elle en garde deux en réserve. Le résultat affiché est un arrondi.

Même si la plupart des exemples utilisent des nombres entiers à un ou deux chiffres, les propriétés et méthodes décrites s’adaptent à tous les nombres réels, hormis le zéro pour les quotients et les nombres négatifs pour les racines carrées.