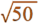Une introduction sans la calculatrice.
1
ère
étape :
Construire un carré de diagonale 10 cm
2
ème
étape :
Calculer l’aire du carré
3
ème
étape :
Calculer le côté du carré
Il sera sans doute nécessaire de rappeler les propriétés des diagonales d’un carré.
La majorité des élèves mesurent le côté et calculent son carré, certains le multiplient même par 4.
On obtient ainsi, 7² = 49 ou 7,1² = 50,41
Avec un peu de chance, des élèves auront trouvé 50 qui est la réponse exacte.
Sinon il faudra la faire apparaître à l’aide des 4 triangles rectangles.
Le côté n’est pas 7 qui est trop petit car 7² < 50, ni 7,1 qui est trop grand car 7,1² > 50
donc c = 7,0 …
On peut calculer de la même manière la deuxième et la troisième décimale.
c = 7,071…
c n’est pas un nombre entier mais ce n’est pas non plus un nombre décimal.
En effet, 7,071² n'est pas un nombre entier donc 7,071² ne peut pas être égal à 50.
c n'est donc pas un nombre à 3 décimales et pour les mêmes raisons ni à 4, ni à 5, etc.
On ne peut donc pas connaître tous les chiffres de c
C'est pourquoi on utilise une notation particulière
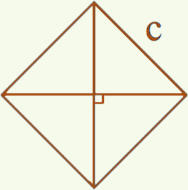
c =
Existe-t-il des nombres plus petits
que leur racine carrée ?
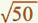
4
ème
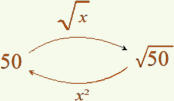
étape : Définition numérique
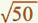
est le nombre positif tel que ( )² = 50