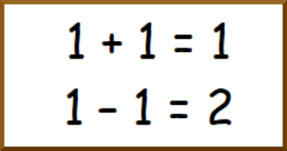Au
commencement
était
l’
addition
:
ajouter
c’est
rassembler
dans
un
même
ensemble des objets considérés comme identiques et interchangeables.
exemple
:
j'ai 15 billes, j'en gagne 7, combien ai-je de billes ?
Il n'est pas nécessaire de poser une addition pour résoudre ce problème,
le
comptage
est la première méthode de calcul.
Tous
les
objets
ne
sont
pas
facilement
manipulables
(
car
trop
lourds,
volumineux,
éloignés
...
),
on
les
remplace
d’abord
par
d’autres
séries
d'objets
(
doigts,
cailloux,
dessins,
symboles
...).
Au
final
on
fait
abstraction
des objets pour additionner directement les nombres (symboles).
On
peut
suivre
la
même
démarche
avec
la
soustraction
,
c’est
à
dire
fabriquer
une
opération
sur
les
nombres
à
partir
d’opérations
sur
les
objets
(enlever, soustraire, éliminer, diminuer, perdre … ).
Nous
pensons
que
des
grandeurs
physiques
ont
leur
place
dans
l'enseignement
des
mathématiques.
Longueurs,
aires
et
volumes
relèvent
de
la
géométrie.
Pourquoi
exclure
masses,
durées,
vitesses,
débits,
masses
volumiques
sous
le
vain
prétexte
qu'ils
relèvent
de la Physique ?
A
moins
qu'on
estime
que
les
calculs
mettant
en
jeu
des
grandeurs
physiques
posent
des
problèmes délicats qu'il est bien agréable de confier au physicien.
Ce
serait,
dans
ce
cas,
chercher
un
refuge
confortable
dans
une
rigueur
mathématique
fallacieuse et glacée. Mais le confort serait-il alors pour l'élève ou pour le professeur ?
APMEP MOTS Tome VI (1982)
L’arithmétique des troupeaux
1°) ‘‘ Les nombres de ’’
2°) Les grandeurs additives
3°) L’algèbre des grandeurs
Les situations et les questions évoluent et c’est là que les problèmes arrivent :
exemple 1 : Aujourd'hui, j'ai perdu 9 billes, il ne m'en reste plus que 3.
J'en avais combien ce matin ?
exemple 2 : Au jeu de l’oie, Catherine lance son dé et recule de 5 cases.
Elle arrive alors sur la case 17. De quelle case est-elle partie ?
exemple 3 : Ce matin, Jean avait 12 images. Son papa lui en donne un paquet.
Maintenant, Jean a 17 images. Combien son papa lui en a-t-il donné ?
Ces
trois
exemples
font
partie
des
problèmes
qui
provoquent
le
plus
grand
nombre
d’échecs
car
l’opération
décrite
dans
l’énoncé
est
l’inverse
de
l’opération à effectuer sur les nombres.
Comme
il
n’est
pas
possible
de
les
séparer
en
problèmes
d’additions
et
problèmes de soustractions, on les regroupe dans le
bloc-additif
.

Avant
de
démarrer
la
transhumance
on
regroupe
les
troupeaux.
Combien
font
1 troupeau + 1 troupeau
?
Au
retour,
chacun
récupère
son
troupeau. Combien font
1 troupeau - 1 troupeau ?
I
l n’existe pas un
sens des opérations
inné comme le sens de l’équilibre par exemple.
La
résolution
de
problèmes
est
un
long
processus
d’apprentissage,
plus
ou
moins
rapide
selon
les
personnes,
qui
s’appuie
sur
les
grandeurs
qui
nous
servent
d’intermédiaires
dans
la
connaissance
du monde qui nous entoure. C’est un processus qui se déroule en trois grandes étapes.
Les mathématiques
de la rue
Dans
une
recherche
menée
au
Brésil,
Schliemann
et
ses
collègues
(1998)
ont
proposé
divers
pro
-
blèmes
à
des
« enfants
de
la
rue »
de
12
ans
environ
qui
n’avaient
ja
-
mais
été
scolarisés
mais
qui
ma
-
niaient
quotidiennement
de
l’argent
pour exercer des petits commerces.
Avec
ces
jeunes
gens,
lorsque
l’on
propose le problème :
«
Quel
est
le
prix
de
3
objets
à
50 cruzeiros l’un ?
»
le taux de réussite est de 75 %.
Or,
lorsqu’on
propose
aux
mêmes
jeunes gens, le problème :
«
Quel
est
le
prix
de
50
objets
à
3 cruzeiros l’un
?
»,
le taux de réussite est de 0 % !
La multiplication entre un nombre entier et une grandeur mesurée, reste une addition répétée.
5 cm + 5 cm + 5 cm = 3 x 5 cm = 5 cm x 3 = 15 cm
On retrouve les trois problèmes types précédents :
- Quelle est la distance parcourue en faisant 3 tours d’une piste de 400 m ?
- Combien de tours d’une piste de 400 m, faut-il faire pour parcourir 1200 m ?
- Si je parcours 1 200 m en 3 tours de piste, quelle est la longueur de la piste ?
Il devient possible de diviser un nombre par un diviseur plus grand que lui, tout d'abord par
l'utilisation des conversions, puis progressivement par l'introduction des nombres décimaux.
4°) Les mathématiques modernes
Les
objets
sont
rarement
identiques.
Pour
les
différencier
on
compare
leurs
grandeurs.
Pour
ces
deux
éprouvettes
par
exemple,
on
peut
mesurer
des
dimensions
(
la
hauteur
d’eau,
le
diamètre
de
l’éprouvette
),
des
quantités
(
le
volume
ou
la
masse de l’eau ), les températures de l’eau …
Les mesures s’expriment comme un nombre d’unités : 5 cm, 28 cl, 17° …
Si
on
transvase
les
quantités
d’eau
dans
la
même
éprouvette,
les
hauteurs
d’eau
ne
s’ajoutent
que
si
les
diamètres
sont
égaux,
les
températures
malheureusement
ne
s’ajoutent
pas
(
on
ne
peut
pas
bouillir
de
l’eau
en
versant
une
casserole
à
40
°
dans
une autre à 60° ), les volumes, eux, sont compatibles avec la somme des liquides.
On peut additionner leur mesure 28 cl + 22 cl,
on effectue le calcul sur les nombres 28 + 22 = 50 .
Les opérations sont ainsi déclinées dans quatre mondes imbriqués :
- le monde physique
- les grandeurs
- les grandeurs mesurées
- les nombres mathématiques
EXERCICE
Combien
de
fois
peut-on
soustraire
8
de
93,
et
combien
reste-t-il à la fin ?
LE BLOC MULTIPLICATIF :
Ici encore, 3 grandeurs en relation génèrent 3 problèmes différents :
- Combien faut-il de joueurs pour faire 4 équipes de basket de 5 joueurs chacune ?
- Combien d'équipes de basket de 5 joueurs peut-on faire dans une classe de 20 élèves ?
- Je répartis 20 élèves en 5 équipes, combien y aura-t-il de joueurs dans chaque équipe ?
Le premier problème permet d’introduire la multiplication comme une addition répétée.
5 joueurs + 5 joueurs + 5 joueurs + 5 joueurs = 4 x 5 joueurs = 20 joueurs
Dans le deuxième problème, on peut procéder par additions répétées jusqu'à arriver à 20.
5 joueurs + 5 joueurs + 5 joueurs + 5 joueurs = 20 joueurs
Dans le troisième problème, l'addition " 5 équipes + 5 équipes + 5 équipes + 5 équipes "
n'a pas de sens. On peut procéder par essais successifs :
si j'en mets 3 par équipe, il m'en faut 5 x 3 joueurs = 15 joueurs ,
je peux en mettre plus, j'essaie 4 ...etc.
C’est la base de l’algorithme utilisé en France pour la division posée. C’est ce même
algorithme qui servira pour le deuxième problème quand les nombres grandiront.
Nous
avons
vu
que
l’on
peut
additionner
ou
soustraire
des
grandeurs
et
les
multiplier
ou
les
diviser
par
un
nombre
entier.
Mais
on
ne
peut
additionner
que
des
grandeurs
homogènes
ou
de
même
dimension,
c’est-à-dire
qui
utilisent
les mêmes unités
.
On peut effectuer
3 m + 8 m
, mais il est impossible de faire
3 m + 5 kg.
De
la
même
façon,
on
a
considéré
pendant
des
siècles
qu’il
était
impossible
de
multiplier deux grandeurs
hétérogènes
:
‘‘En multipliant des
heures
, on ne peut pas obtenir des
mètres
.’’
Pierre
Varignon
est
le
premier
à
oser
calculer
avec
des
grandeurs
non
homogènes.
Le
5
juillet
1698,
à
l'Académie
des
sciences,
il
définit
la
vitesse
comme
le
rapport
d'une
longueur
sur
un
temps.
Tout
d'un
coup,
la
vitesse
devient
une
grandeur
physique.
Cela
marque
la
véritable
naissance
d’une
algèbre
des
grandeurs
dont
les
relations
se
décrivent
à
l’aide
de
formules
respectant les « équations aux dimensions » en référence au
système métrique
.
Les élèves de collège peuvent ainsi rencontrer :
des grandeurs quotients :
des rapports :
quotient de deux grandeurs homogènes
des grandeurs produits
Aire d’un rectangle = longueur x largeur = 5 m x 3 m = 15 m²
LE BLOC MULTIPLICATIF :
L’enseignement
des
problèmes
additifs
ne
s’arrête
pas
à
l’école
primaire.
Des
nouvelles
situations
et
des
grandeurs
en
plus
grand
nombre, augmentent la difficulté.
Il
devient
souhaitable
de
proposer
des
notations
et
des
représentations
efficaces.
Voici une sélection
de problèmes additifs
proposés en 6ème.


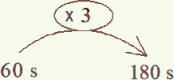

Les conversions :
3 min = 3 x 60 s = 180 s
Ce paquet de 8 yaourts coûte 2 €.
Quel est le prix d’un yaourt ?


Attention
ce diagramme est faux
car 3 min x 60 = 180 min
On peut calculer avec des
grandeurs sans les mesurer.
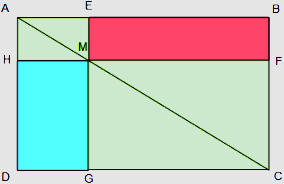
Quel est le plus grand des rectangles,
le rouge ou le bleu ?
GRANDEUR (Mathématique)
Voilà
un
de
ces
mots
dont
tout
le
monde
croit
avoir
une
idée
nette,
et
qu'il
est
pourtant
difficile
de
bien
définir.
Ne
serait-ce
pas
parce
que
l'idée
que
ce
mot
renferme,
est
plus
simple
que
les
idées
par
lesquelles
on
peut
entreprendre
de
l'expliquer ?
D'Alembert- L’Encyclopédie
«
Aujourd’hui,
la
science
mathématique
s’est
largement
affranchie
de
la
question
des
grandeurs.
Théoriquement,
les
mathématiques
peuvent
donc
à
la
fois
se
transmettre
et
se
développer
sans
référence à la notion de grandeur.
En
mathématiques,
on
ne
travaille
pas
sur
les
grandeurs
(c’est
l’objet
d’autres
disciplines,
comme
la
physique,
la
technologie,
les
sciences
de
la
vie
et
de
la
Terre
ou
la
géographie
et
l’économie
par
exemple),
mais
avec
les
grandeurs
ou
à
partir
d’elles.
En
mathématiques,
on
travaille
dans
le
domaine des nombres
».
Programme de 3e. Place des grandeurs dans l’enseignement des mathématiques au collège.
Ce point de vue ne fait pas l’unanimité chez les mathématiciens.
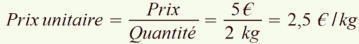
Ces formules se prêtent aux transformations algébriques indépendamment des unités.
si alors et
si alors et
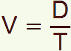
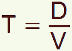
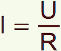


Elles
sont
entièrement
reconstruites
à
partir
des
entiers,
de
la
théorie
des
ensembles
infinis
de
Cantor
et
de
la
logique
formelle.
Le
recours
à
l'intuition
géométrique
ou
physique
est
banni.
La
notion
de
grandeur
est
renvoyée
au
domaine
de
la
physique,
même
les
considérations
de
mouvement
ou
de
temps
sont
exclues.
Ce
changement
consommera
le divorce entre les
mathématiques « modernes »
et la
physique
.
Le
XIX
éme
siècle
est
l'âge
d'or
des
mathématiques
portées
par
les
sciences
physiques :
cinématique, optique, acoustique, chaleur, électricité, magnétisme ….
Les
applications
se
développent
rapidement
dans
tous
les
domaines,
laissant
croire
que
la
science
peut
tout.
Beaucoup
de
propriétés
sont
considérées
comme
allant
de
soi,
la
justification s’obtient a posteriori, par les succès obtenus.
Cet
édifice
est
progressivement
ébranlé
par
l'apparition
des
géométries
non-euclidiennes
et
des
phénomènes
pathologiques
liés
à
l'infini
.
Il
devenait
urgent
de
refonder
les
mathématiques pour retrouver la rigueur.
En
1970
en
France,
c’est
cette
Mathématique
Moderne
destinée
à
des
mathématiciens
professionnels qui est imposée à tous les élèves de la maternelle à l’université.
Face
à
l’échec,
le
programme
de
1978
réintroduit
la
géométrie
et
les
grandeurs
à
l’école
élémentaire et au collège, mais pas à n’importe quelle place :

Les largeurs, hauteurs, épaisseurs et profon-
deurs, ont la dimension d’une longueur.
Evitez cependant de dire en classe :
« une largeur est une longueur ».



Exemple
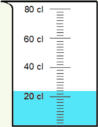
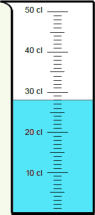
A la première question, beaucoup répondent 17 cl en lisant la hauteur de l’objet.
Pour la deuxième, beaucoup calculent 39 cl - 22 cl

La confusion entre ces différents mondes est une source d’erreurs importante.
Extrait
A la foire
Un
homme
achète
un
cheval
pour
600 € puis le revend 700 €.
Il
le
rachète
plus
tard
pour
800
€
et le revend 900 €.
Combien a-t-il gagné d’argent ?