C’est cette question, à la une de journaux pendant quelques années qui m’a inspiré cette enquête.
Les enfants sont-ils toujours plus grands que leurs parents ?
Introduction
Recueil des données
Traitements
Prolongements

En 2000, j’ai lancé l’enquête dans les classes de 4
ème
et 3
ème
du collège.
Chaque élève devait demander à au moins 10 personnes de plus de 18 ans, leur taille et celle de leurs parents.
Ils établissent globalement la répartition des effectifs
de chaque caractère indépendamment des autres.
On peut la représenter par des histogrammes.
On constate un décalage vers la droite pour les fils,
ce que confirme le calcul des moyennes.
Mais
en
procédant
ainsi,
on
a
perdu
de
l’information
car
on a rompu la correspondance entre un fils et son père.
On ne peut pas répondre à la question :
y a-t-il beaucoup de fils plus petits que leurs pères ?
Pour cela il faut traiter les écarts individuellement.
Les tris à plat
Les écarts indiduels
Les nuages de points
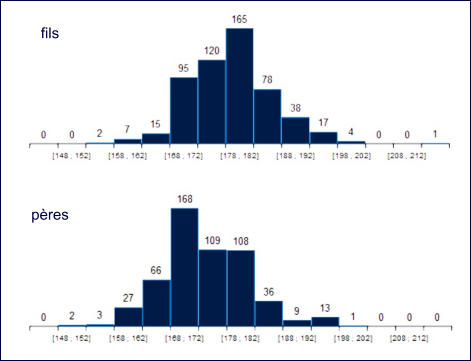
Moyenne = 178,3
Moyenne = 173,6
Les fils mesurent en moyenne 5 cm de plus que leurs pères.

Le dépouillement peut se faire de deux manières non-exclusives :
- par classe, en répartissant le travail par groupes.
- Sur un tableur où chaque élève entre ses données.
Les filles mesurent en moyenne 4 cm de plus que leur mère,
et 6 cm de moins que leur père.
23 % sont plus petites que leur mère.
77 % sont plus petites que leur père.
23 % des filles sont plus petites que leur mère.
Les garçons mesurent en moyenne 5 cm de plus que leur père,
et 14 cm de plus que leur mère.
22 % sont plus petits que leur père.
4 % sont plus petits que leur mère.
Résultats :
Reste
à
savoir
si
les
filles
plus
petites
que
leur
mère
sont
grandes
ou
petites.
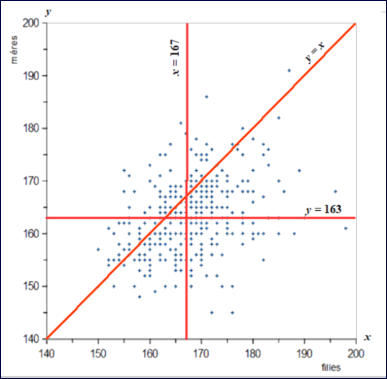
Un outil bien adapté est le nuage de points facilement obtenu sur le
tableur
.
Le
graphique
est
distribué
sans
les
droites.
Chaque
point
représente
une
fille
interrogée, les coordonnées sont sa taille et la taille de sa mère.
- Le problème posé aux élèves est de distinguer sur le graphique
les filles grandes des filles petites.
- Même question pour les mères.
- Enfin comment distinguer les filles plus petites que leur mère,
des filles plus grandes que leur mère ?
L’emploi
de
droites
n’est
pas
du
tout
évident
pour
les
élèves,
d’autant
que
certains
sont
perturbés
par
le
petit
triangle,
ils veulent absolument que les trois droites soient concourantes.
On peut aussi en profiter pour introduire les équations de droites.
On termine en demandant aux élèves de caractériser chacune des régions obtenues.
Par exemple, la région
A
: ce sont des filles grandes, mais plus petites que leur mère qui est grande.
A


La taille qu’atteindra un enfant à l’âge adulte, est en partie conditionnée par celle de ses parents. Pour se faire une idée plus précise,
les nouveaux carnets de santé proposent depuis 2018 aux parents un calcul très simple, appelée la formule de Tanner.
Elle est basée sur la moyenne des tailles des parents à laquelle ont ajoute 6,5 cm pour les garçons et on enlève 6,5 cm pour les filles.
Ce calcul comporte une marge d’erreur évaluée à 6 cm en plus ou en moins et elle est atteinte dans à peu près deux tiers des cas.
Cette taille cible n’est donc pas un indicateur d’une grande précision.
C’est que les prédispositions génétiques n’expliquent pas tout, si c’était le cas, toutes les filles ou tous les garçons d'une même
famille auraient la même taille.
Si on applique cette formule à notre population, on obtient les graphiques ci-dessous.
Ils représentent les écarts entre la taille réelle et la taille cible calculée avec la formule de Tanner.
Par exemple 42 % des filles sont plus grandes que la taille prévue.
On constate un décalage assez prononcé vers la droite. L’explication est peut-être dans la différence de période.
Les statistiques utilisées pour la formule de Tanner sont récentes. La différence de taille entre les générations a peut-être disparue.


