Recueil des données
Traitements
Prolongements

Introduction
Problème :
Je vais lancer 2 dés, vous devez deviner leur somme.
Quel nombre vaut-il mieux choisir ?
Pour répondre à la question, j’ai d’abord demandé aux élèves ce qu’ils en pensaient a priori.
Les réponses sont très diverses avec une préférence pour le 12 ou le 7 mais aussi « on ne peut pas prévoir car c’est le hasard ».
J’ai ensuite demandé à chacun de faire l’expérimentation à la maison.
Chaque élève devait lancer 50 fois deux dés et noter ses résultats sur sa fiche qui servira aussi pour les prolongements.
C’est une activité fondatrice des probabilités dans la mesure
où elle montre que l’on peut parfois prédire le hasard.






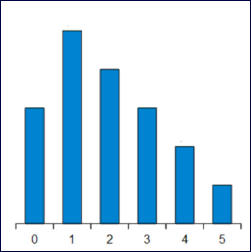
Pour rassembler les données, les élèves passaient successivement inscrire leurs réponses
sur une feuille de tableur projetée au tableau.
Le graphique se construisait au fur et à mesure, l’ambiance était celle d’une arrivée de
course où chacun soutenait son favori.
Modèle 1
Au final plusieurs élèves ont déclaré « c’est normal, il y a plus de manières de faire 7 »,
et ils ont cité
ces trois manières de faire 7 :
(1 + 6 )
( 2 + 5 )
( 3 + 4 )
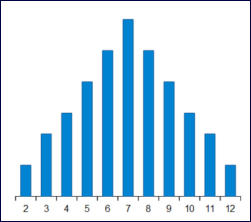
Ce qui s’est traduit par un tableau et un graphique.
Modèle 2
J’ai dû proposer de distinguer les deux dés et de compter six manières de faire 7 :
(1 + 6 )
( 2 + 5 )
( 3 + 4 )
(6 + 1 )
( 5 + 2 )
( 4 + 3 )
En conclusion, le Modèle 2 explique bien mieux la situation
et le tableau à double entrée appuie encore cette idée.
La fiche de réponse permet une nouvelle étude sans relancer les dés.
J’ai choisi l’écart car la solution est moins intuitive qu’avec d’autres opérations ( différence, maximum, minimum, produit )
Cette fois ci le tableau permet d’anticiper l’expérimentation qui intervient comme une validation.