On peut en distinguer plusieurs formes.
Les distributions
Les quantiles
Les valeurs extrêmes sont souvent mal connues et correspondent à des situations très particulières peu représentatives de l’ensemble de la population. Pour les bas salaires, on trouve des temps partiels, des autoentrepreneurs, des détenus … Pour les hauts salaires, la part en nature est difficile à estimer : prime, véhicule, logement, frais de représentation … C’est pour cela que l’INSEE n’utilise pas le minimum ou le maximum mais les premier et dernier déciles.
Les moyennes
Le premier traitement est la construction du tableau d’effectifs et de son graphique associé : l’histogramme. Il est construit sur deux axes : l’axe de la variable et l’axe des effectifs.
Les écarts ou les rapports inter-déciles Pour les salaires, nous avons déjà rencontré le rapport interdécile (D9 / D1) qui est un indice de leur dispersion ( ‘‘ l’éventail des salaires ’’) et permet de mesurer l’évolution des inégalités au cours du temps. Pour les petites séries, on peut se contenter de l’écart interquartile (Q3 - Q1), simple et rapide, il donne déjà beaucoup d’informations.
Pour utiliser ces distributions, il est nécessaire de les caractériser par des indicateurs chiffrés.
Le calcul des moyennes
Trois définitions 1°) La moyenne est la somme des valeurs divisée par le nombre de valeurs. 2°) La moyenne peut remplacer toutes les valeurs en conservant la somme. 3°) La somme des écarts à la moyenne est nulle. soit Autrement dit les écarts positifs compensent exactement les écarts négatifs.
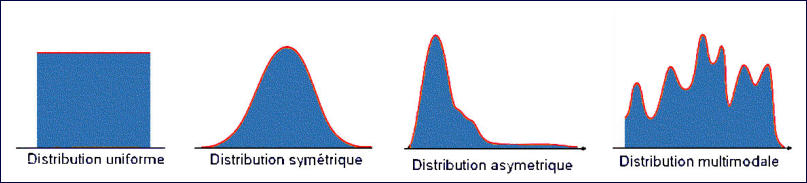
Une manière simple d’obtenir des indicateurs sans calcul, est d’utiliser les effectifs. La population, rangée par valeurs croissantes, est partagées en groupes d’effectifs égaux. Les quantiles sont les limites de ces groupes.
Les moyennes pondérées
On ne connaît souvent une série statistique que par son tableau d’effectifs où les valeurs de la variable se trouvent en première colonne. Pour calculer la moyenne, il faut tenir compte du poids de chaque valeur qui est déterminé par l’effectif dans la deuxième colonne. Par exemple, le nombre d’enfants dans les familles à 3 enfants est 3 x 18 = 54
Par exemple en médecine, lors d'une prise de sang, vous avez dû remarquer sur la feuille de résultats des « valeurs de référence » à côté de vos mesures. Cet intervalle regroupe les valeurs obtenues par la très grande majorité des personnes en bonne santé.
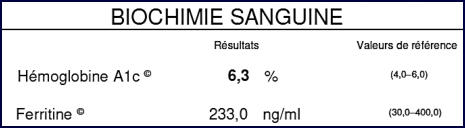
Si vos résultats se trouvent hors de l’intervalle, cela indique un risque de développer une pathologie. Il sera d’autant plus élevé que votre résultat sera éloigné des valeurs de référence.
Quel est le centre de cette barre ?
Correction
L’envie est grande de vouloir caractériser une population par un seul nombre. Par exemple, on entend souvent que la température du corps humain est 37°. En réalité elle se situe entre 36° et 38° car nous n’avons pas tous la même température. 37° a l’avantage d’être un nombre simple et de se trouver au ‘‘milieu’’ des valeurs possibles, par contre il ne donne aucune information sur la répartition. La médiane est une autre valeur centrale au ‘‘milieu’’ des effectifs, mais la plus connue est la moyenne .
Les indicateurs de dispersion
L’étendue Enseignée au collège, c’est sans aucun doute la plus simple ( étendue = maximum - minimum ) mais dans la réalité elle n’est pas utilisée car elle ne dépend que deux valeurs souvent peu fiables.
L’écart-type C’est l’indicateur de dispersion associé à la moyenne. Nous avons déjà vu que la somme des écarts à la moyenne est nulle et donc leur moyenne aussi.
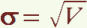
Pour éviter les écarts négatifs la solution adoptée est d'utiliser les carrés. La moyenne des carrés des écarts à la moyenne s'appelle la variance . La variance n'a pas la même dimension que la variable. Si celle-ci est, par exemple, une longueur en m, la variance s'exprime en m². Pour retrouver la dimension de la variable, on prend la racine carrée de la variance et on obtient l'écart type.
Comme on le voit, le calcul est très lourd et il ne s’effectue pas à la main mais sur une calculatrice ou un tableur. Un écart type faible indique que les valeurs sont regroupées autour de la moyenne, tandis qu’un écart type élevé indique une grande dispersion des valeurs. Il tient son importance de son utilisation en statistiques inférentielles.
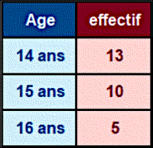
Voici en cours d'année, la répartition par âge dans une classe de 3 ème . Quel est l'âge moyen des élèves de cette classe ?
Test
Histogrammes et intervalles
Moyenne ou médiane ?
Une   pyramide   des   âges   est   un   histogramme   double où l’axe de la variable est vertical.
L’objectif des statistiques est de réduire la quantité de données. Ronald Fisher
Dans cet exemple, les salaires sont regroupés par tranche de 100 €. La hauteur des rectangles est proportionnelle à l’effectif .
Une manière simple et efficace pour réduire les données est de les regrouper par intervalle de même largeur.
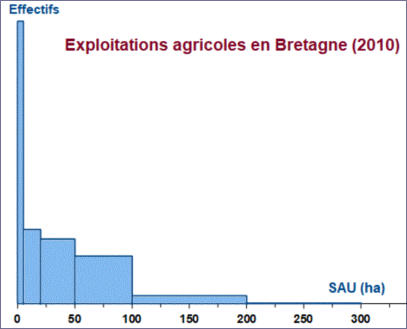
Il n’est pas obligatoire de choisir des tranches de même largeur, mais dans ce cas l’histogramme change de nature, les hauteurs ne sont plus proportionnelles à l’effectif mais à l’aire de chaque tranche.
feuille de calcul à télécharger
Remarque Il est possible d’utiliser la densité comme axe pour repérer la hauteur des rectangles mais on peut aussi se contenter d’un seul axe en utilisant leur aire.
calcul des hauteurs
On calcule d’abord la densité de chaque intervalle en divisant l’effectif par la largeur, on obtient l’effectif moyen pour une tranche-unité. Toutes ces tranches ayant même largeur, leur hauteur est proportionnelle à leur effectif c’est-à-dire la densité. Il reste à choisir une échelle pour que le graphique ait une taille convenable. Ici j’ai choisi 1 cm pour une densité de 200.
La notion de densité étant délicate à interpréter, certains préfèrent utiliser les diagrammes en boîtes ( avec ou sans moustaches ). Les tranches ont toutes une même largeur arbitraire et sont limitées par des quantiles. Il n’y a donc aucun calcul à effectuer ! La lecture se base sur le positionnement de la médiane et sur les écarts inter-quantiles.
Traitements numériques d’une variable